Activité 1 - Étude d'un tremplin de ski

Présentation de l'activité

  • Références au programme :
    • Seconde: Étudier l’alignement de trois points dans le plan.
    • Seconde: Déterminer une équation de droite passant par deux points donnés.
    • Seconde: Algorithme de calcul approché de longueur d’une portion de courbe représentative de fonction.
  • Prérequis :
    • Équations de droites.
    • Images et antécédents.
    • Distances entre deux points.
  • Description L'étude de la structure d'un tremplin de saut à ski permet de réexploiter les notions d'alignement, d'équations droites et de fonction. On étudie la forme du tremplin, la hauteur des supports et la longueur de la piste.

Situation

Une station de sports d'hiver souhaite construire un tremplin de saut à ski dont la structure est en acier. Le profil de la piste est représenté dans un plan rapporté à un repère orthonormal $(O, I,J)$. L’unité est le mètre. La piste d’envol du tremplin est constituée de 2 parties :

• une partie représentée par un segment $[AB]$.

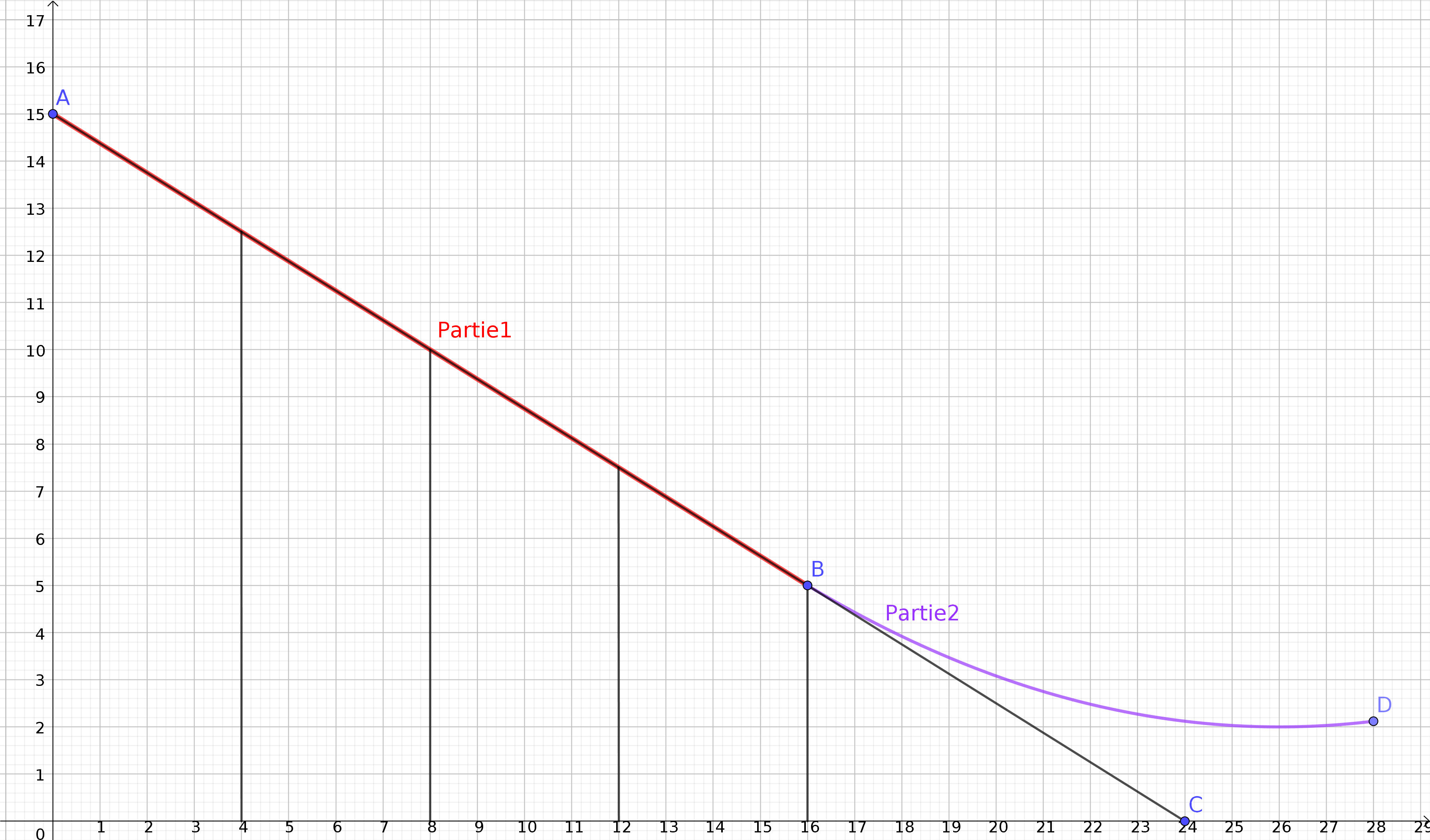
• une partie représentée par un arc de parabole $\overset{\frown}{BD}$ . Il faut qu’il y ait raccordement au point $B$. tremplin.png

Étude de la partie $[AB]$

La première partie est portée par un support rectiligne passant par le point $A$ de coordonnées $(0,15)$ et le point $C$ de coordonnées $(24,0)$. Le raccordement entre les deux parties doit se faire au point $B$ de coordonnées $(16,5)$.

Alignement de trois points

La fonction alignement permet de vérifier si trois points de coordonnées entières sont alignés. Elle prend les coordonnées entières des trois points en paramètres et renvoie un booléen.

In [1]:
def alignement(x1,y1,x2,y2,x3,y3):
    determinant=(x2-x1)*(y3-y1)-(y2-y1)*(x3-x1)
    if determinant==0:
        rep=True
    else:
        rep=False
    return rep
alignement(0,15,24,0,16,5)
Out[1]:
True
Remarques didactiques

La fonction proposée fonctionne bien avec des arguments entiers, il n'en serait pas de même avec des flottants (des nombres réels). En effet, le test d'égalité == est mis en défaut sur les flottants. Par exemple 0.1 + 0.1 + 0.1 == 0.3 s'évalue en False. Cela est dû à la représentation en machine des flottants, qui ne permet pas d'utiliser des valeurs exactes.

On pourrait remplacer

if determinant==0:
    rep=True
else:
    rep=False

par rep = (determinant == 0).

Suggestions pédagogiques

  • Compléter un programme

    Le programme précédent étant fourni en remplaçant les lignes 2,3,4 et 6 par determinant= ...,if... ,rep= ... et rep= ..., demander aux élèves de compléter les lignes 2,3,4 et 6 de la fonction.

  • Tester la fonction précédente pour vérifier l'alignement des points A,B et C.

Hauteurs des poteaux

La première partie du tremplin est supportée par des poteaux placés tous les quatre mètres (abscisses : 4, 8 et 12). On souhaite déterminer la hauteur de ses poteaux.

Équation de droite

La fonction equation donne les coefficients $a$ et $b$ de l'équation réduite $y=ax+b$ d'une droite passant par deux points d'abscisses différentes. Elle prend les coordonnées des deux points en paramètres et renvoie les valeurs de $a$ et $b$.

In [2]:
def equation(xA,yA,xB,yB):
    assert xB!=xA, "il faut donner deux points d'abscisses distinctes"
    a=(yB-yA)/(xB-xA)
    b=yA-a*xA
    return a,b
a,b = equation(0,15,24,0)
print(a,b)

-0.625 15.0
Remarques didactiques

L'utilisation de assert permet de vérifier que les abscisses des deux points sont distinctes.

Dans le cas contraire, assert interrompt le déroulement de l'exécution et affiche le message "il faut donner deux points d'abscisses distinctes".

Suggestions pédagogiques

  • Compléter un programme

    Le programme précédent étant fourni en remplaçant les lignes 3 et 4 par a= ...et b= ..., demander aux élèves de compléter les lignes 3 et 4 de la fonction equation.

  • Tester la fonction equation afin d'obtenir le coefficient directeur et l'ordonnée à l'origine de la droite $(AB)$.

Image par une fonction affine

La fonction suivante détermine l'image d'un réel $x$ par une fonction affine d'équation $ g(x)=ax+b$. Elle prend les valeurs de $a$ et $b$ et celle de $x$ en paramètres et renvoie l'image de $x$. On l'appelle ensuite pour $x=4$, pour $x=8$, et pour $x=12$ avec les paramètres correspondant à l'équation de la droite de la première partie du tremplin pour déterminer la hauteur des poteaux.

In [3]:
def fonctionAffine(a,b,x):
    y=a*x+b
    return(y)

print("Hauteur du premier poteau =",fonctionAffine(a,b,4),"m")
print("Hauteur du seconde poteau =",fonctionAffine(a,b,8),"m")
print("Hauteur du troisième poteau =",fonctionAffine(a,b,12),"m")

Hauteur du premier poteau = 12.5 m
Hauteur du seconde poteau = 10.0 m
Hauteur du troisième poteau = 7.5 m
Suggestions pédagogiques

  • Écrire un programme

    Écrire une fonction fonctionAffine qui prend $a$, $b$, $x$ en paramètres et qui renvoie $ax+b$.

  • Tester la fonction fonctionAffine afin de calculer les hauteurs des poteaux.
Remarque

Les coefficients $a$ et $b$ de $(AB)$ ont déjà été calculés.

Longueur de la piste sur la partie $[AB]$.

Afin de placer le revêtement sur la piste, on souhaite connaître sa longueur totale. La fonction suivante calcule la longueur d'un segment $[AB]$ dans un repère orthonormal $(O,I,J)$. Elle prend les coordonnées des points $A$ et $B$ en paramètres et renvoie la longueur de la piste en unités de longueur.

In [4]:
import math
def longueur(x1,y1,x2,y2):
    d=math.sqrt((x1-x2)**2+(y1-y2)**2)
    return d
print("La longueur AB est égale à", longueur(0,15,16,5),"mètres.")

La longueur AB est égale à 18.867962264113206 mètres.
Suggestions pédagogiques

  • Écrire un programme

    Écrire une fonction longueur qui prend en paramètres les coordonnées $x_1$, $y_1$, $x_2$, $y_2$ des extrémités d'un segment et renvoie sa longueur.

  • Tester la fonction longueur afin d'estimer la longueur de la piste $[AB]$.
Remarque

La fonction sqrt de la bibliothèque math permet de calculer la racine carrée d'un nombre. Il est également possible d'utiliser la syntaxe x**(1/2).

Étude de la partie $\overset{\frown}{BD}$

La deuxième partie du tremplin est un arc de parabole d'équation $f(x)=0{,}03x^2 - 1{,}56x + 22{,}28$. L'abscisse du point $D$ est égale à $28$.

Coordonnées de D

La fonction suivante calcule l'image d'un réel $x$ par la fonction $f$. Celle-ci permet de déterminer l'ordonnée de $D$.

In [5]:
def f(x):
    return 0.03*x**2-1.56*x+22.28
print(f(28))

2.120000000000001
Suggestions pédagogiques

  • Écrire un programme

    Écrire une fonction f prenant en paramètre un nombre $x$ et renvoyant son image par la fonction (mathématique) $f$.

  • Tester la fonction pour calculer l'ordonnée de $D$
  • Interpréter le résultat (expliquer le nombre de décimales).

Longueur de l'arc $\overset{\frown}{BD}$.

Pour calculer la longueur totale du revêtement, on souhaite évaluer également la longueur de la deuxième partie de la piste.

Pour cela, on divise l'intervalle $[16;28]$ en $n$ intervalles de longueur $\frac{(28-16)}{n}=\frac{12}{n}$. On place alors les points $A_0$,$A_1$,$A_2$,...$A_n$ de la courbe d'abscisses respectives :

$16$; $16+\frac{12}{n}$; $16+2\times\frac{12}{n}$;...; $28$.

Pour calculer une valeur approchée de notre portion de courbe, il suffit alors de faire la somme des longueurs des segments $[A_i;A_{i+1}]$.

In [6]:
def LongueurArc(n,borneInf,borneSup):
    longueurTotale=0
    x1=borneInf
    pas=(borneSup-borneInf)/n
    x2=x1+pas
    for i in range(n):
        y1=f(x1)
        y2=f(x2)
        longueurTotale=longueurTotale+longueur(x1,y1,x2,y2)
        x1=x1+pas
        x2=x2+pas
    return longueurTotale
print(LongueurArc(10,16,28))  

12.573667317776675
Suggestions pédagogiques
  • Expliquer un programme
Expliquer les lignes 2 à 8.

  • Compléter un programme

    Le programme précédent étant fourni en remplaçant la ligne 9 par longueurTotale = ..., demander aux élèves de compléter la ligne 9.

  • Compléter un programme

    Le programme précédent étant fourni en remplaçant les lignes 10 et 11 par x1 = ... et x2 = ..., demander aux élèves de compléter les lignes 10 et 11 pour passer au segment suivant.

  • Tester la fonction longueurArc pour calculer la longueur de l'arc $\overset{\frown}{BD}$ avec différentes valeurs de $n$ (nombre d'intervalles).

Animation susceptible d'être présentée aux élèves

Les programmes suivants sont à destination de l'enseignant et permettent d'illustrer en classe la convergence de la longueur approchée.

In [7]:
import matplotlib.pyplot as plt
#Points
def listePoints(n,borneInf,borneSup):
    pas=(borneSup-borneInf)/n
    listeAbscisses=[borneInf+i*pas for i in range(n+1)]
    listeOrdonnees=[f(x) for x in listeAbscisses]
    return listeAbscisses,listeOrdonnees
def longueurApprochee(n,borneInf,borneSup):
    liste=[]
    for i in range(1,n):
        liste.append(LongueurArc(i,borneInf,borneSup))
    return liste
In [8]:
import matplotlib.animation
from IPython.display import HTML

#cte
N = 15

lX,lY=listePoints(1000,16,28)
fig, (ax1, ax2) = plt.subplots(1, 2,figsize=(15, 6))
ax1.plot(lX,lY,'r--')
ax1.set_title('Courbe approchée',color="#1e7fcb",fontsize=14)
ax2.set_title('Approximation longueur',color="#1e7fcb",fontsize=14)
courbeSegments, = ax1.plot([],[],'.-',color="#1e7fcb")
courbeConvergence, = ax2.plot([],[],color="#1e7fcb")
ax2.set_xlim(( 0, N))
ax2.set_ylim((12.5, 12.6))


def init():
    global courbeSegments,courbeConvergence
    courbeSegments.set_data([], [])
    courbeConvergence.set_data([], [])
    return (courbeSegments,) 

def animate(i):
    global courbeSegments,courbeConvergence
    lx,ly=listePoints(i+1,16,28)
    courbeSegments.set_data(lx,ly)
    valeurs = longueurApprochee(i+2,16,28)
    courbeConvergence.set_data(range(1,i+2),valeurs)
    ax1.set_title('Courbe approchée - nombre de Segments:{}'.format(i+1))
    ax2.set_title('Approximation longueur $\simeq${:.3f}'.format(valeurs[-1]))
    return (courbeSegments,)
  

plt.close ()
ani = matplotlib.animation.FuncAnimation(fig, animate, frames=N,init_func=init,blit=False,interval=750)
# l'un ou l'autre
HTML(ani.to_jshtml())
#HTML(ani.to_html5_video())
Out[8]:


Once Loop Reflect